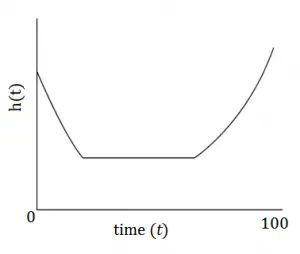
En análisis de la supervivencia se llama función de riesgo a una función que mide la probabilidad de que a un individuo le ocurra cierto suceso de interés a lo largo del tiempo. En fiabilidad de sistemas, donde el suceso de interés suele ser el fallo de un dispositivo, se suele denominar a esta función tasa de fallo.
Definición
Sea una variable aleatoria definida sobre el intervalo [0, ∞) que indica el tiempo de sobrevivencia de un determinado objeto, dicho de otro modo, hasta que se produzca el primera fallo. Sea su función de distribución. Entonces, la probabilidad que un objeto presente un fallo antes de un tiempo , puede expresarse como:
Donde es la función de confiabilidad o supervivencia, es decir, la probabilidad que un determinado objeto sobreviva más allá de un tiempo .
Si es su correspondiente función de densidad, es decir,
entonces la función de riesgo es
Ejemplo
Si la supervivencia está regida por una distribución exponencial de parámetro , entonces,
y la función de riesgo es
Por lo tanto, en este caso la función de riesgo es constante en el tiempo.
Bibliografía
- Borges, R. (2005). Análisis de sobrevivencia utilizando el Lenguaje R. XV Simposio de Estadística, Paipa, Colombia. Disponible en PDF